Transformer 구조에서 Layer Norm 이 Batch Norm이 더 적합한 이유

 

 

 

Batch Normalization

https://arxiv.org/pdf/1502.03167

 

 

Background

batch normalizaion 은 2015년에 제시된 ICS(Internal Covariate Shift) 문제를 줄일 수 있는 아이디어입니다. covariate shift 는 학습 때 활용한 데이터가 실제 추론에 사용되는 데이터간의 분포가 다르면 추론 성능에 악영향을 미칠 수 있다라는 주장인데 이게 신경망 내부에서도 발생할 것이다 라는 주장을 하며 생긴용어가 Internal Covariate Shift 라고 합니다. 아래 사진을 보면 직관적으로 이해가 될 것 같습니다. 신경망을 통과하면서 데이터의 분포가 달라지는 현상이 발생하는데

 

통과하는 레이어 수가 많아질수록 그 정도가 심해지기 때문에 당연히 추론이나 학습 성능에 문제가 생길 확률이 큽니다. Batch Normalizaion 은 기존의 정규화 과정에서 학습데이터마다 분포가 다른것을 배치별로 평균과 분산을 활용해 정규화하는 것 입니다.

나동빈님의 영상을 참고하여 알게 된 batch normalizaion가 현실에서는 하이퍼파라미터 의존도를 줄였으며, 학습속도를 향상시키고, 모델이 일반적으로 즉, 학습데이터에만 태스크를 잘 처리하도록 하는것이 아닌 실제 현상을 잘 반영시키게 된 효과가 있었다고 합니다.

그런데 논문에서는 ics 를 감소시킨다고 주장하였으나 실제로 증명하지는 못했다고 합니다. 그래서 그것을 증명하기 위한 How Does Batch Normalization Help Optimization?  라는 논문이 나왔습니다.

https://arxiv.org/pdf/1805.11604

 

 

우선 일반적으로 Batch Norm 을 적용시킨 네트워크가 Accuracy 가 가파른 폭으로 올라갔다는 것을 보여줍니다.

 

 

우측의 히스토그램을 보면 각 레이어의 분포를 나타내고 있는데요 가장우측의 Standard + Noisy BatchNorm 에서 Layer3 부터 분포가 갑작스럽게 변하여 ICS가 발생하고 있음을 볼 수 있습니다. ICS가 발생하고 있음에도 불구하고 왼쪽 그래프를 보면 학습성능이 우수함을 볼 수 있습니다.

즉 임의로 Batch Norm Layer 이후 바로 Noise 를 넣어 covariate shift 를 발생시켰을 때에도 BatchNorm 이 포함된 네트워크는 일반적인 네트워크보다 성능이 우수함을 보였습니다. 그래서 실험적으로 Batch Norm 이 ICS 문제를 해소할 수 있다는 이전 논문의 반박을 하였고, 심지어 ICS가 크게 발생함에도 불구하고 Batch Norm 이 있으면 성능이 좋아진다는 것을 보여준 사례가 되었습니다.

해당논문에서 ICS를 파라미터의 기울기 계산하여 ICS를 계산하는 방법을 제안했는데, 포스팅의 목적보다 너무 벗어나는것 같아 다루지 않겠습니다. 궁금하신분께서는 논문을 참고하시면 될 것 같습니다.

그렇다면 ICS 를 해소하지 못했음에도 불구하고 성능이 좋은 이유는 뭘까요? 논문에서는 Batch Norm 의 Smoothing 효과 때문이라고 설명합니다.

 

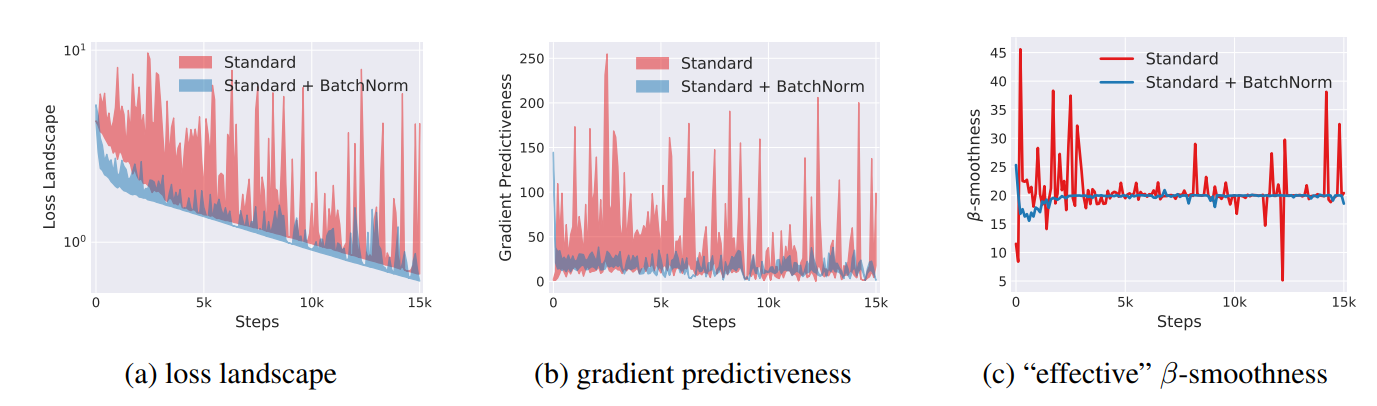
Loss Landscape 가 훨씬 더 예상 가능한 범위로 형성되면서 학습효과가 증대된다고 말하고 있습니다.

 

 

Batch Normalization Layer

미니배치의 평균값과 분산을 구해서 normalizaion 을 수행할 수 있습니다. 그리고 감마와 베타를 활용해 실제 output 을 내는데요, 여기서 감마와 베타가 실제 학습에 활용되는 파라미터입니다. 학습중에는 loss 를 최소화 하는 방향으로 감마와 베타를 찾아갈 것 입니다.

정규화에서 학습 파라미터를 사용하는 이유는 활성화 함수의 특징에 있습니다. sigmoid를 예시로 들면 어떤 구간에서는 매우 선형적으로 작동하기 때문에 표준정규분포로 정규화한 0과 1사이의 값에서 선형적으로 작동하게 됩니다. 그래서 감마와 베타를 활용해 non-linearity 를 지켜주고, 해당 정규화 레이어의 output 도 적절하게 내보낼 수 있게됩니다. 결론은 레이어의 입력을 정규화할 때는 linearity 를 주의해서 정규화 해야한다는 점 입니다.

 

Batch Normalization Layer 연산구분

batch normalization Layer 는 학습할때와 추론할 때 네트워크에서의 역할이 달라집니다. 학습할때 감마와 베타 파라미터를 학습시켜야 하지만 추론때에는 필요없습니다. 따라 해당 파라미터들을 고정하여 학습된 파라미터에 의한 값이 나와야합니다.

 

step 7 에서부터는 BN 이 training 모드로 네트워크에 있었던 것을 inference 모드로 바꿉니다. ( 파라미터 고정을 통해서 )

Batch Normalization Data Flow

입력 데이터 (X)

 

$$

X = \begin{bmatrix} [1,\ 2] \ [2,\ 4] \ [3,\ 6] \end{bmatrix}

$$

배치로 들어온 데이터

shape: (3, 2)

→ 샘플 3개, 각 샘플은 2차원 벡터

---

Linear Layer 통과

가중치와 bias를 이렇게 두겠습니:

$$ [ W = \begin{bmatrix} [1,0], \ [0,1] \end{bmatrix}, \quad b = [0,\ 0] ] $$

즉, 아무 변화 없는 선형층

$$ [ Z = XW + b = X ] $$

결과:

Z =
[
 [1, 2],
 [2, 4],
 [3, 6]
]

shape 그대로 (3, 2)

---

Batch Normalization

1️⃣ Batch Mean (μ)

feature별 평균:

$$ μ=[(1+2+3)/3, (2+4+6)/3]=[2, 4] $$

---

2️⃣ Batch Variance (σ²)

$$ σ2=[((1−2)2+(2−2)2+(3−2)2)/3,((2−4)2+(4−4)2+(6−4)2)/3]=[2/3, 8/3] $$

---

3️⃣ Normalize (x̂)

$$ \hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} (ε 무시한다고 가정) $$

샘플별 계산

첫 번째 샘플

$$ [1,2] → [-1/\sqrt{2/3},\ -2/\sqrt{8/3}] ≈ [-1.22,\ -1.22] $$

두 번째

$$ [2,4] → [0,\ 0] $$

세 번째

$$ [3,6] → [1.22,\ 1.22] $$

결과:

X_hat =
[
 [-1.22, -1.22],
 [ 0.00,  0.00],
 [ 1.22,  1.22]
]

그리고 해당값에 gamma 와 betta 연산을 통해 Layer 를 통과시킵니다. 이처럼 batch norm 은 미니 배치의 피처별로 평균, 분산을 구해서 원본 데이터에 대입시키는 방법으로 Normalizaion 을 수행하게 됩니다.

Layer Normalization

arxiv.org

Layer Normalization 은 Batch Norm 이 RNN 에 적용하기 어려운 문제점을 해소하기 위해 제시된 방법입니다. RNN은 시간단위로 계산을 합니다. 따라서 미니배치의 각 피쳐마다 통계를 이용해 정규화하는 BN 의 경우에는 해당 스트림의 맥락을 반영하지 못합니다.

가장 큰 문제는 RNN 이나 NLP, 혹은 음성데이터의 경우는 배치마다 길이가 다릅니다.

샘플 1: "나는 밥을 먹었다"        (길이 4)
샘플 2: "오늘"                    (길이 1)
샘플 3: "어제 비가 와서 우산을 썼다" (길이 6)

이것을 BN 을 활용한 Layer output 을 사용한다면 샘플2 의 2,3 샘플1의 3,4 가 0이 됩니다. 그렇기 때문에 데이터의 의미를 충분히 반영하지 못하는 문제가 발생합니다. 이 문제는 시계열 데이터에도 그대로 적용됩니다. 이미지나 성적통계(국어는 국어끼리, 수학은 수학끼리) 와 같은 데이터가 아니라 피쳐하나가 다른 피쳐나 데이터에도 영향을 주는경우는 Batch 사이즈에 영향을 받지 않고 데이터의 의미를 잘 반영할 수 있는 LN 이 성능이 좋다고 주장합니다.

 

BN 과의 차이점

Batch Normalization은 미니배치 단위로 평균과 분산을 계산하여 정규화를 수행합니다. 반면 **Layer Normalization(LN)**은 이름 그대로 레이어 단위, 정확히는 하나의 샘플 내부 feature들에 대해서만 정규화를 수행합니다. 즉, 정규화의 기준이 완전히 다릅니다.

• Batch Normalization
  • 평균, 분산 계산 축: batch 방향
  • 같은 feature를 가진 여러 샘플을 함께 사용
• Layer Normalization
  • 평균, 분산 계산 축: feature 방향
  • 하나의 샘플 안에서만 계산

하나의 샘플 x = [x₁, x₂, ..., xₐ]에 대해:

$$ \mu = \frac{1}{d} \sum_{i=1}^{d} x_i $$

$$ \sigma^2 = \frac{1}{d} \sum_{i=1}^{d} (x_i - \mu)^2 $$

$$ \hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} $$

그리고 Batch Normalization과 동일하게 scale, shift 파라미터를 적용합니다:

$$ y_i = \gamma_i \hat{x}_i + \beta_i $$

여기서 중요한 점은 γ, β는 feature 차원에 대해서만 존재하며 batch 크기와 무관하다는 것입니다.

위의 수식대로 같은 샘플을 가지고 레이어를 통과하는 연산을 수행해보겠습니다.

Layer Normalization Data Flow

입력 데이터 (X)

$$ X = \begin{bmatrix} [1,\ 2] \\ [2,\ 4] \\ [3,\ 6] \end{bmatrix} $$

shape: (3, 2)

→ 샘플 3개, 각 샘플은 2차원 벡터

---

Linear Layer 통과

가중치와 bias는 이전과 동일하게 설정합니다.

$$ Z = X $$

---

Layer Normalization 적용

Layer Normalization은 각 샘플마다 독립적으로 평균과 분산을 계산합니다.

첫 번째 샘플 [1, 2]

$$ \mu = (1 + 2) / 2 = 1.5 $$

$$ \sigma^2 = ((1 - 1.5)^2 + (2 - 1.5)^2) / 2 = 0.25 $$

정규화 결과:

$$ [1, 2] \rightarrow [-1, 1] $$

---

두 번째 샘플 [2, 4]

$$ \mu = 3,\quad \sigma^2 = 1 $$

정규화 결과:

$$ [2, 4] \rightarrow [-1, 1] $$

---

세 번째 샘플 [3, 6]

$$ \mu = 4.5,\quad \sigma^2 = 2.25 $$

정규화 결과:

$$ [3, 6] \rightarrow [-1, 1] $$

---

Layer Normalization 결과

X_hat =
[
 [-1,  1],
 [-1,  1],
 [-1,  1]
]

Transformer 구조에서 Layer Normalization 이 Batch Normalization 보다 적합한 이유

1. 시퀀스 길이 가변성과 Masking 문제

Transformer의 Self-Attention은 가변 길이 시퀀스를 처리해야 합니다. 입력형태는 각 문장마다 길이가 다르다는 점입니다. 이를 해결하기 위해 짧은 문장에는 padding을 추가하 attention mask를 사용해야 합니다.

Batch Normalization을 이러한 구조에 적용하면 심각한 문제가 발생합니다. BN은 배치와 시퀀스 차원 전체에 걸쳐 평균과 분산을 계산하는데 위에서 봤던 것 처럼 의미 없는 padding 토큰의 0 벡터가 통계에 포함됩니다. 결과적으로 문장 길이에 따라 정규화 통계가 왜곡되고, 같은 내용의 문장이라도 padding의 양에 따라 다르게 정규화될 수 있습니다.

 

 

반면 Layer Normalization은 각 토큰의 feature 차원에 대해서만 정규화를 수행합니다. 즉, 하나의 토큰 내부에서만 평균과 분산을 계산하기 때문에 padding 토큰이나 시퀀스 길이가 정규화 통계에 전혀 영향을 미치지 않습니다. 각 토큰은 독립적으로 정규화되므로 데이터의 의미가 충실히 반영되고 배치나 시퀀스 구조와 무관하게 일관된 정규화가 가능합니다.

2. Autoregressive Decoding과 배치 크기 불일치

Transformer Decoder는 추론 시 미래의 정보를 참조하지 못하도록 autoregressive 방식으로 동작합니다. 즉, 이전에 생성한 토큰을 바탕으로 다음 토큰을 하나씩 순차적으로 생성합니다. 이 과정에서 대부분의 경우 배치 크기가 1이 됩니다. 이는 Layer Normalization 논문에서 보여준것처럼 Batch Normalization에 치명적인 문제를 야기합니다.

Layer Normalization은 배치 크기와 무관하게 안정적으로 동작합니다. 배치 크기가 1이든 32든 정규화 결과는 일관되며, 학습 시 관찰한 성능이 추론 시에도 그대로 유지됩니다. 이는 Transformer Decoder의 생성 품질에 결정적으로 중요한 특성입니다.

3. Residual Connection과의 구조적 불일치

Transformer의 각 블록은 residual connection을 사용합니다: y = x + Sublayer(LN(x)). 이 구조가 중요한 이유는 gradient의 흐름 때문입니다. 역전파 시 ∂y/∂x = 1 + ∂Sublayer/∂x 가 되어, gradient가 항상 직접 흐를 수 있는 경로(identity mapping)가 보장됩니다. 이는 깊은 네트워크에서 gradient vanishing 문제를 해결하는 핵심 메커니즘입니다.

만약 Batch Normalization을 residual path에 사용하면, BN의 출력이 배치 통계에 의존하기 때문에 residual path에 batch-dependent noise가 주입됩니다. 이는 gradient flow를 불안정하게 만들고, 특히 깊은 Transformer에서는 gradient 폭발이나 소실을 일으킬 수 있습니다. 실제로 Post-LN Transformer(residual 후에 LN을 적용)는 레이어가 깊어질수록 학습이 불안정해지는 것으로 알려져 있으며, Pre-LN Transformer(residual 전에 LN을 적용)가 더 안정적인 학습을 보입니다. BN은 이러한 residual connection의 특성과 근본적으로 충돌합니다.

Layer Normalization은 각 샘플을 독립적으로 정규화하기 때문에 배치에 의존하지 않습니다. 따라서 residual path의 gradient flow를 방해하지 않으며, 수십 개의 레이어로 이루어진 깊은 Transformer에서도 안정적인 학습이 가능합니다. 이러한 구조적 조화가 Transformer가 Layer Normalization을 사용하는 또 다른 중요한 이유입니다.